Web-Schrödinger 3.0

Iratkozz fel a levelezőlistára, hogy értesülj a Web-Schrödingerrel kapcsolatos hírekről (új verzió, példák stb.)

Bevezetés

A Web-Schrödinger egy, stacionárius (időfüggetlen) és az időfüggő Schrödinger egyenlet megoldására szolgáló interaktív program. A program maga egy alkalmazásszerveren fut és egyszerű web böngésző segítségével (Internet Explorer, Mozilla, Opera, Chrome, stb) érhető el. A felhasználónak nem kell semmit telepítenie a saját gépén. A felhasználó betöltheti és futtathatja az előre elkészített példákat és változtathat azok beállításain, továbbá készíthet teljesen új példákat, melyek mentése a saját számítógépre szintén lehetséges..

A program eléréséhez kattints ide!

Elméleti háttér
A program használata
Levelezőlista
"A" függelék: Példák
Példa fájl pályázat !
Hivatkozások

Elméleti háttér

Időfüggő Schrödinger egyenlet

A ψ(r;t) hullámfüggvény időfejlődését a kvantummechanikában az időfüggő Schrödinger egyenlet határozza meg:

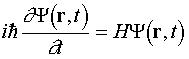
time dependent Schroedinger equation

ahol r = (x,y) a helykoordináta, t az idő, H = K + V a Hamilton operator, ahol K mozgási energia operátora és V = V(x,y) a helyzeti energia operátora.

Ha ismert a V(x,y) potenciál függvény és a ψ(x,y,t₀) = ψ₀(x,y) kezdeti hullámfüggvény,akkor az időfüggő Schrödinger egyenlet segítségével bármely későbbi időpillanatra meg tudjuk határozni a ψ(x,y,t) hullámfüggvényt. A hullámfüggvényből az összes megfigyelhető mennyiséget ki lehet számítani, például a rho(x,y,t) megtalálási valószínűségsűrűséget és a j(x,y,t) áramsűrűséget.

Időfüggetlen Schrödinger egyenlet

A rho(x,y,t) megtalálási valószínűségsűrűség megadja annak valószínűségét, hogy a kvantummechanikai részecskét az (x,y) pont környezetében találjuk meg a t időpontban. Azokat a ψ(x,y,t)=ψ(x,y) állapotokat, ahol ψ(x,y) egy időfüggetlen függvény, stacionárius állapotoknak nevezzük, ezek az időfüggetlen (stacionárius) Schrödinger egyenlet megoldásai:

Hψ(r) = Eψ(r)

ahol E az állapot energiája.

A program használata

A program összes funkciója a menürendszerből érhető el a felhasználó számára. A program indításakor egy alapértelmezett beállítás töltődik be, ezt a felhasználó azonnal képes futtatni a Time development menün keresztül vagy betölthet más beállításokat a File menü Load Example és Load menüpontjai segítségével. Az összes paraméter változtatható az Edit menü segítségével, s ezek a beállítások bármikor menthetőek is a File menü Save menüpontjában.

A menürendszer felépítése

Files

Load Example

Az ebben a menüpontban betölthető páldák a kvantummechanika legfontosabb jelenségeit mutatják be, köztük a hullámcsomag szétfolyását, az alagutazást, a kötött állapotokat, stb. A jelenlegi lista, a Függelék "A" részében található, ezeknek a példáknak a száma természetesen folyamatosan bővül a frissítésekkor. A felhasználó a példa betöltése után végignézheti a betöltött paramétereket és módosíthat is rajtuk az Edit menü segítségével, mielőtt futtatná a szimulációt a Calculation menüből.

Load

A felhasználó ebben a menüpontban képes saját számítógépéről beállításokat tartalmazó fájl feltöltésére. Ilyen paraméter fájl elkészíthető beállítások mentése folyamán (Save menüpont), de a megfelelő formátumú fájl szövegszerkesztő programmal is létrehozható.

Save

A paraméterek aktuális beállításait a felhasználó bármikor elmentheti a saját számítógépére.

Edit

Mesh

A program a hullámfüggvényt és a potenciált egy kétdimenziós rács pontjaiban adott számértékekkel, azaz mátrixként kezeli. Ebben a menüpontban a felhasználó meghatározhatja a pontok számát ezen a hálón (N_x , N_y) az x és y irányokban, továbbá megadhatja a számolási tartomány méretét Angström-ben (s_x, s_y). Az ezekből származtatható Δx = s_x/N_x, Δy = s_y/N_y felosztás értékek tipikus alkalmazás esetén 0.1 - 1 Å közé esnek. A koordinátarendszer középpontja a számolási tartomány közepén található.

A numerikus algoritmus periodikus határfeltételt használ, aminek következtében, ha a hullámcsomag elhagyja a számolási az egyik oldalon, az bejön az ellenkező oldalon. Ez olyan, mintha ’kicsempéznénk’ az egész síkot a számolási tartománnyal. Ennek következtében mikor a hullámcsomag eléri a számolási doboz határát, szembetalálkozik a szomszédos „csempében” létező másolatával, ami fizikailag értelmetlen interferenciákat okoz. A paraméterek beállításainál (térbeli és időbeli felosztás, potenciál, kezdeti állapot) ügyelni kell, hogy ez a jelenség ne történjen meg.

V₀ adja meg a potenciál háttér értékét elektronvoltban (eV).

Megjegyzés: az időfüggő- és az időfüggetlen Schrödinger egyenlet megoldásánál alkalmazott eltérő algoritmusok miatt általában az időfüggő számoláshoz finomabb rács szükséges. Legtöbb esetben Nx=256 megfelelő érték az időfüggő- és Nx=64 az időfüggetlen számoláshoz.

Potential

A V(x,y) potenciált a felhasználó különböző alakzatokból (kör, téglalap, sík) rakhatja össze interaktív módon. Bármennyi alakzat elhelyezhető ezekből a síkon. Az alakzatok geometriai paramétereit és a hozzájuk tartozó potenciál értékeket is a felhasználó állíthatja be. Azoknál a rácspontoknál, ahol több alakzat átfedi egymást, a potenciál értékét a legutoljára odahelyezett alakzat potenciál értéke határozza meg. A program minden lépésben megmutatja az adott alakzatok által létrehozott potenciálfüggvényt.

Initial state

Itt tudja a felhasználó meghatározni a kezdeti ψ₀(x,y) hullámcsomagot, amely az időfüggő számolás kezdőállapota (az időfüggetlen számolás nem használja az itt beállított ψ₀ függvényt). A kezdeti hullámfüggvény egy un. csonkított síkhullám [7] hullámcsomag, ami nem más, mint egy Gauss hullámcsomag és egy négyszög ablakfüggvény konvoluciója. A program együtt ábrázolja egy összetett színű képen a beállított kezdeti hullámfüggvény megtalálási valószínűségsűrűségét és a potenciálfüggvényt. Ahhoz, hogy biztosítsuk a hullámfüggvény megfelelő alakját (minimális méret, lapos felületű burkoló), amikor az a potenciálhoz ér, a kezdeti állapot készítésénél egy idő késleltetési algoritmust építettünk be a programba. A felhasználó megadja bx, by távolságokat, melyekből a gép kiszámolja a késleltetési időt, ezáltal a hullámfüggvény alakja pontosan akkorra válik „ideálissá”, mikor időfejlődése során elérkezik a potenciálhoz.

ax, ay határozza meg a hullámcsomag térbeli szélességét. A kezdeti állapotot úgy kell megadni, hogy a potenciál alakzatokkal való átfedése elhanyagolhatóan kicsi legyen.

Detectors

Ebben a menüpontban a felhasználó vízszintes és függőleges szakaszokat (detektorokat) helyezhet el a számolási ablakban. A hullámcsomag időfejlesztése során a program kiszámítja az ezeken a szakaszokon áthaladó I(t) valószínűségi áramsűrűséget, továbbá ennek T időintegrálját a teljes számolt időre. A T mennyiséget transzmissziónak hívjuk, ugyanis ez megadja annak valószínűségét, hogy a kvantumrészecske áthalad az adott szakaszon (detektoron).

Calculation parameters

Itt tudjuk megadni az időfüggő és az időfüggetlen számítás paramétereit.

Az időfüggő számítás paraméterei:
Az időlépések számát Nt , az időlépésközt Δt beállításával változtathatja a felhasználó. Δt megadása atomi egységekben történik, 1 au = 0.0242 fs (femtoszekundum).

A numerikus algoritmus korlátot szab meg a maximálisan használható Δt értékre:: Δt < 4/π (Δx)² / D, ahol D a számolás dimenziószáma, D=2 kétdiemnzióban. (Ez az összefüggés atomi mértékegységben érvényes, azaz Δx értéke Bohr-ban értendő, 1 Bohr = 0.529 Å. Az alapértelmezett Δx = 0.3 Å felosztás esetén a fenti számolás alapján Δt = 0.2 au egy alkalmas lépésköz választás, s ez látható alapértelmezett beállításként.)

Mint látható, a számolás pontossága finom időbeli felosztást igényel, emiatt az eredménynél nem volna célszerű minden lépés után megjeleníteni a számolt hullámfüggvényt. Ezért a felhasználó beállíthatja ennek a megjelenítésnek a lépésközét (display timestep).

Az időfüggetlen számítás paraméterei:
Nstat a kiszámítandó állapotok száma.

Calculation

Time development

Amikor a felhasználó a „RUN” gombot megnyomja, a szerveren elkezdődik az időfejlődés számítása. A számítási folyamat a megjelenő linkre kattintva, kis képeken figyelhető meg. Tipikus paraméterek beállítása esetén a számolás 1-2 percet vesz igénybe. (Ha egyidejűleg több számítás is fut a szerveren – ugyanattól a felhasználótól vagy másoktól – a számítás lassabb lehet. A program kiírja az egyidejűleg futó számítások számát a „RUN” gomb megnyomása után -- ha egynél több számolás fut éppen.)

Eigenstates

Amikor a felhasználó a „RUN” gombot megnyomja, a szerveren elkezdődik a stacionárius állapotok (sajátállapotok) kiszámítása. A számolás néhány másodpercig, vagy percig tart, a számolási rács méretétől és a kiszámítandó állapotok számától függően. (Ha egyidejűleg több számítás is fut a szerveren – ugyanattól a felhasználótól vagy másoktól – a számítás lassabb lehet. A program kiírja az egyidejűleg futó számítások számát a „RUN” gomb megnyomása után -- ha egynél több számolás fut éppen.) Amikor a számítás véget ér, a program kiírja az állapotok energiáit és megjeleníti a hullámfüggvényeket.

Results

Miután a szerver befejezte a teljes időfejlődés számítását, a program egy összetett színű képen jeleníti meg a megtalálási valószínűségsűrűség időfejlődését. Ehhez a program első lépésben megkeresi a megtalálási valószínűség időbeli maximumát és ezzel az értékkel normálja az összes képkockát. Továbbá, a program, hogy lehetővé tegye a nagyobb és kisebb valószínűségsűrűség értékek egyszerre való ábrázolását, egy nemlineáris színskálát (γ=2.5) használ.

Ha a felhasználó detektorokat is elhelyezett a számítási ablakban, a program az ezeken a detektorokon áthaladó I(t) áramsűrűség függvényeket is megjeleníti, valamint kiírja a detektorokhoz tartozó T transzmisszió értékeket.

Levelezőlista

Iratkozz fel a levelezőlistára, hogy értesülj a Web-Schrödingerrel kapcsolatos hírekről (új verzió, példák stb.).

"A" függelék: Példák

A példákat két csoportra osztottuk, az időfüggő- és az időfüggetlen számoláshoz tartozó példákra. Semmi sem akadályozza meg, hogy ugyanarra a példára időfejlődést és sajátállapotokat is számoltassunk a programmal, de a "time development" csoportba tartozó példák az időfejlődés szempontjából érdekes eseteket, a "stationary states" csoportba tartozó példák pedig a stacionárius állapotok szempontjából érdekes eseteket mutatnak be. Bizonyos esetekre, mint például a potenciál doboz, mind az időfüggő, mind az időfüggetlen számolás tanulságos eredményeket ad.

A példákat úgy terveztük meg, hogy a számítási módszerből adódó periodikus határfeltétel ne befolyásolja az eredményeket. E célból az időfejlődés számolásoknál úgy választottuk az időskálát, hogy a számolás még azelőtt végetérjen, mielőtt a hullámcsomag eléri a számolási doboz szélét. A stacionárius állapot számolásoknál pedig egy potenciálfalat helyeztünk a számolási doboz széleire.

Az időfüggő számoláshoz tartozó példák

band_1D_allowed

A wave packet is approaching a periodic potential with energy in the allowed band. The wave packet is passing through the potential.

band_1D_forbidden

Egy hullámcsomag, melynek energiája a tiltott sávba esik, megközelít egy periodikus potenciált. A hullámcsomag visszaverődik a potenciálról.

hardcore

Hullámcsomag szóródása rögzített, kör alakú potenciálon. Figyeljük meg a kifutó hullám hengerszimmetrikus komponensét!

quantum_revival

A „quantum revival” (újjászületés) jelenségének bemutatása.

stm_on_nanotube

Szén nanocső pásztázó alagútmikroszkópos leképezésének szimulációja. Részletesen erről lásd [3].

tunneling_oblique

Hullámcsomag áthaladása potenciálfalon keresztül, ahol V>E. A hullámcsomag 75^o szögben ütközik a falnak.

tunneling_perpendicular

Hullámcsomag áthaladása potenciálfalon keresztül, ahol V>E. A hullámcsomag 90^o szögben ütközik a falnak.

Az időfüggetlen számoláshoz tartozó példák

box

Téglalap alakú potenciáldoboz sajátállapotai.

circle

Köralakú potenciáldoboz sajátállapotai.

step

Ebben a példában egy potenciállépcsőt helyeztünk el a potenciáldobozba. A bal oldalon kicsit nagyobb a potenciál értéke, mint a jobb oldalon.

Példa fájl pályázat

Készíts saját példát valamilyen érdekes kvantummechanikai jelenség demonstrálására! Ezután küld el a mentett paraméterfájlt a következő E-mail címre, mark@sunserv.kfki.hu. A legjobb példa fájlok felkerülnek a Web-Schrödinger példa könyvtárába. Kérlek, küld el a rövid leírását is az általad készített példának!

Hivatkozások

Tudománynépszerűsítő cikkek és előadások

Márk Géza, Biró László: Egy hullámcsomag kalandjai az alagútmikroszkópban;
Fizikai Szemle, 2006. június
http://www.nanotechnology.hu/preprint/FizSzemle_2006_06_WavePacket.pdf
Vancsó Péter, Biró László, Márk Géza: Kvantum főnix -- hullámcsomag dinamika az Interneten;
Fizikai Szemle, 2009. július-augusztus
http://www.nanotechnology.hu/reprint/FizSzemle_2009_07-08_WebSchroedinger.pdf
Márk Géza István, Vancsó Péter, Philippe Lambin, Biró László Péter: Utazások alagúteffektussal;
MFA Nylt Nap, 2010. november 12. video előadás
http://www.nanotechnology.hu/online/2010_alagutazas/index.html

Tudományos publikációk

Schrödinger equation; (in several languages)
http://en.wikipedia.org/wiki/Schroedinger_equation
Time development of quantum mechanical systems; (1995-) (English and Hungarian)
http://www.kfki.hu/~mark/physedu/schrodinger/index.html
Márk, Géza, I.; Biró, László, P.; Gyulai, József: Simulation of STM images of 3D surfaces and comparison with experimental data: carbon nanotubes;
Phys. Rev. B 58, 12645(1998).
http://ojps.aip.org/journal_cgi/getabs?KEY=PRBMDO&cvips=PRBMDO000058000019012645000001&gifs=No
http://www.nanotechnology.hu/reprint/prb_58_12645.pdf
Márk, Géza, I.; Biró, László, P.; Gyulai, József; Thiry, Paul, A.; Lucas, Amand, A.; Lambin, Philippe: Simulation of scanning tunneling spectroscopy of supported carbon nanotubes;
Phys. Rev. B 62, 2797(2000).
http://ojps.aip.org/journal_cgi/getabs?KEY=PRBMDO&cvips=PRBMDO000062000004002797000001&gifs=Yes
http://www.nanotechnology.hu/reprint/prb_62_2797.pdf
Lambin, Philippe; Márk, Géza, I.; Meunier, Vincent; Biró, László, P.: Computation of STM images of carbon nanotubes;
Int. J. Qunatum.. Chem. 95, 495(2003).
http://www3.interscience.wiley.com/cgi-bin/abstract/104528199/ABSTRACT
http://www.nanotechnology.hu/reprint/IntJQuantChem_95_493_STMSimul.pdf
Márk, Géza, I.; Biró, László, P.; Lambin, Philippe: Calculation of axial charge spreading in carbon nanotubes and nanotube Y-junctions during STM measurement;
Phys. Rev. B 70, 115423-1(2004).
http://scitation.aip.org/getabs/servlet/GetabsServlet?prog=normal&id=PRBMDO000070000011115423000001&idtype=cvips&gifs=yes
http://www.nanotechnology.hu/reprint/prb_70_115423_3d.pdf
Géza I. Márk PhD Thesis, FUNDP Namur, 2006.
http://www.mfa.kfki.hu/~mark/phd/index.html
Márk, Géza, I.; Vancsó, Péter; Hwang, Chanyong; Lambin, Philippe; Biró, László, P.: Anisotropic dynamics of charge carriers in graphene;
Phys. Rev. B 85, 125443-1(2012).
http://link.aps.org/doi/10.1103/PhysRevB.85.125443
http://www.nanotechnology.hu/reprint/prb_85_125443_graphene_anisotropy_2012.pdf
Vancsó, Péter; Márk, Géza, István; Hwang, Chanyong; Lambin, Philippe; Biró, László, P.: Time and energy dependent dynamics of the STM tip – graphene system;
European Journal of Physics B 85, 142-1(2012)
http://www.springerlink.com/content/g8vm5758262v274n/?MUD=MP
http://www.nanotechnology.hu/reprint/epjb_85_142_graphene_jellium_2012.pdf
Márk, Géza, I.; Vancsó, Péter; Lambin, Philippe; Hwang, Chanyong; Biró, László, P.: Forming electronic waveguides from graphene grain boundaries;
Journal of Nanophotonics 6, 061719-1(2012)
http://nanophotonics.spiedigitallibrary.org/article.aspx?articleid=1476909
http://www.nanotechnology.hu/reprint/jnanophot_6_061718_waveguide2012.pdf
S. Janecek, E. Krotscheck: A fast and simple program for solving local Schrödinger equations in two and three dimensions;
Comput. Phys. Comm. 178 (11) (2008) 835–842.
http://www.sciencedirect.com/science/article/pii/S0010465508000453
S.A. Chin, S. Janecek, and E. Krotscheck: An arbitrary order diffusion algorithm for solving Schrödinger equations;
Computer Physics Communications 180 (2009) 1700–1708.
http://www.sciencedirect.com/science/article/pii/S0010465509001131

Utolsó módosítás : 2013. február 14. by Géza I. Márk , mark@sunserv.kfki.hu
This page was accessed

times since Feb 8, 2013.