Next: Discussion Up: Simulation of STM images Previous: Geometric line cut

Quantum line cut

We have performed quantum mechanical probability current calculations through a simple two dimensional (2D) jellium potential modeling the STM tip - nanotube - support system. STM constant current feedback loop was simulated by moving the tip along a line (''quantum line cut'' ) where the transferred probability was constant.

The 2D model potential has the value zero outside the effective surfaces of the electrodes and the value $-9.81 \, eV$ inside. ( $E_F = 5 \, eV$ , $W = 4.81 \, eV$ ).

Tunneling probability is calculated from time dependent scattering of a Gaussian wave packet approaching the model potential from the bulk of the tip. The $\vec j (x,z,t)$ probability current density was calculated along a horizontal line inside the support bulk (at $z_j = -0.5 \, nm$ ). Line integration of $\vec j (x,z,t)$ along this line gives the I(t) probability current and the tunneling probability is obtained as $P_{tunnel} = \int_0^{t_{max}} I(t) dt$ .

Probability density of the scattered wave packet is shown on Fig. 6..

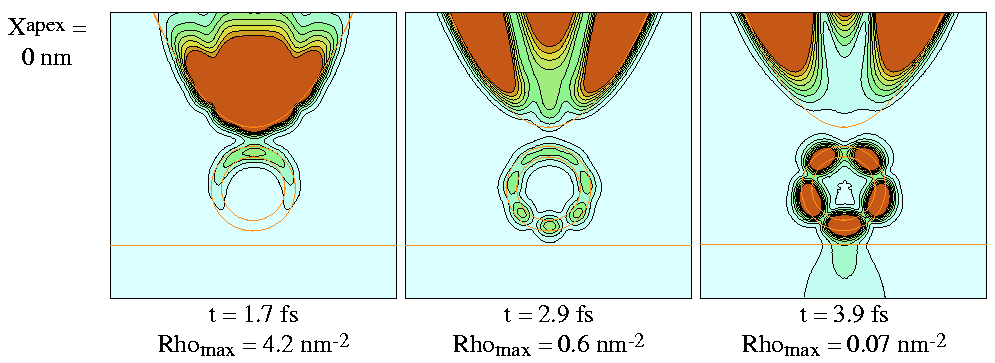
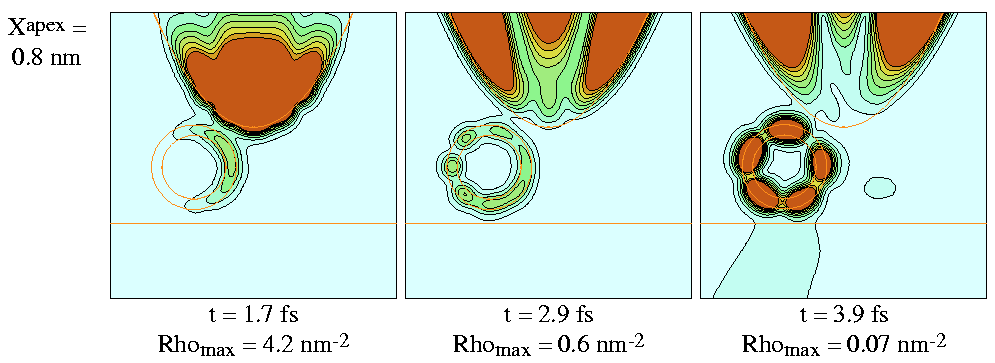
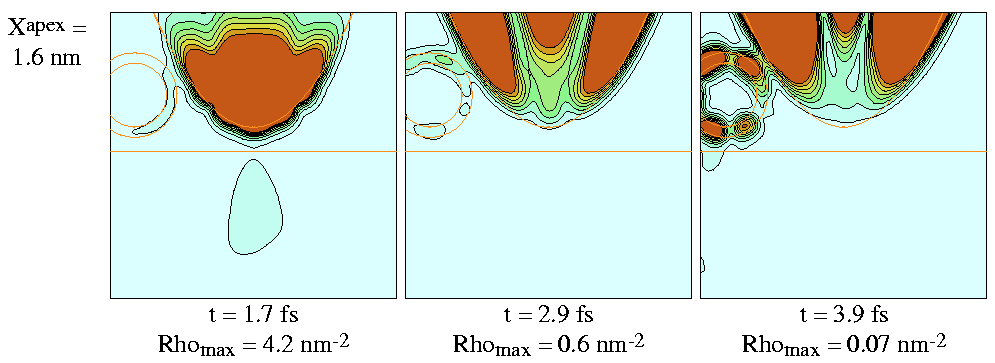
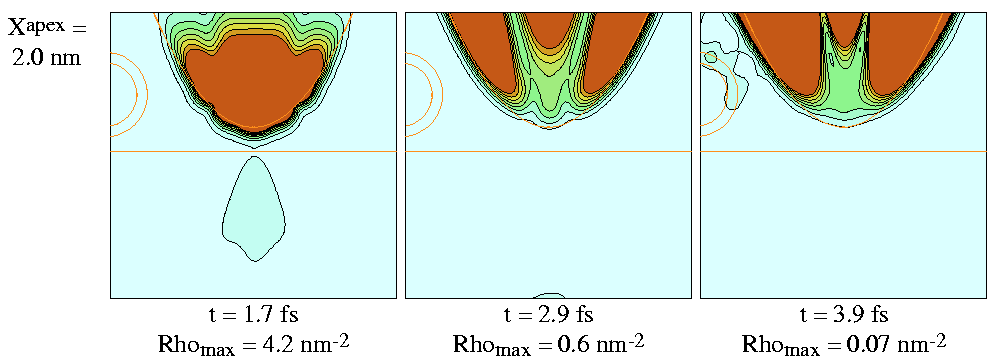
Figure 6: Probability density of scattered wave packet for selected time instants and for selected X_apex lateral tip displacements. Effective surfaces of electrodes are shown by red lines. Size of presentation window is $3.84 \, nm$ . Contour lines are drawn on sqare root scale. Each frame is normalized to its maximum density. Initial momentum of Gaussian wave packet is $k_z = - \sqrt{{ 2 E_F} / m_e } = -11.46 \, {nm} ^ {-1}$ and its initial with is $\Delta k_x = \Delta k_z = 1.336 \, {nm} ^ {-1}$ .

For $X_{apex} = 2 \, nm$ the tip is far from the nanotube. Wave packet is tunneling simply from the tip apex into to plane support.
For $X_{apex} = 0 \, nm$ tip is above the uppermost point of nanotube. It is a resonant tunneling situation. The probability which remained in the tube region forms standing waves and is leaking into the tip and into the support in distinct impulses[6].
For $X_{apex} = 0.8 \, nm$ (oblique incidence) majority of the probability flows out of the tip at its side around the nearest points of the sample and tip.
For $X_{apex} = 1.6 \, nm$ we can observe switching of the tunneling points.

**Table I:** Average time t_spent (in fs) the quantum particle spends in different regions. ''Forbidden'' region is the region of zero potential. t_spent for ''total interface'' region is sum of the values for ''forbidden'' and ''tube'' regions.
X_apex (nm)	Forbidden	Tube	Total Interface = Forbidden + Tube
0.0	0.071	0.084	0.155
0.8	0.079	0.123	0.202
1.6	0.060	0.020	0.080
2.0	0.057	0.0001	0.057

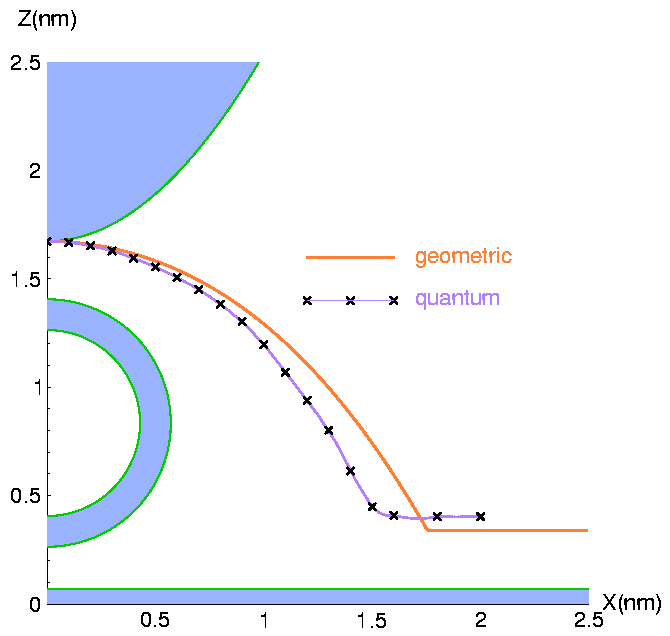
STM constant current loop was simulated by finding for each fixed X_apex lateral tip displacement that appropriate Z_apex vertical tip displacement which yielded a setpoint tunneling probability value of $P_{setpoint} = 3 \cdot 10^{-3}$ . ( X_apex , Z_apex ) tip displacement values resulting from this procedure are shown on Fig. 7. by crosses.

Figure 7: Comparison of geometric and quantum line cut. Thick red line is the geometric line cut. Crosses show calculated points of quantum line cut.

Next: Discussion Up: Simulation of STM images Previous: Geometric line cut