 |
 |
 |
 |
x = 0.0 nm | x = 0.8 nm | x = 1.6 nm | x = 2.0 nm |

|
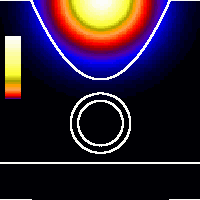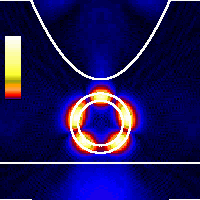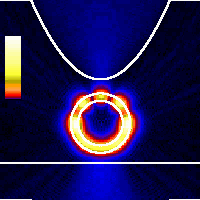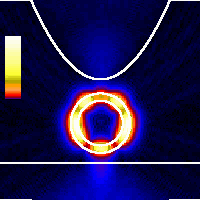
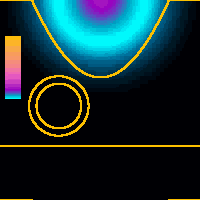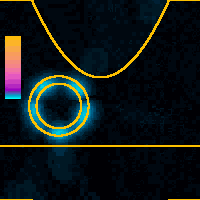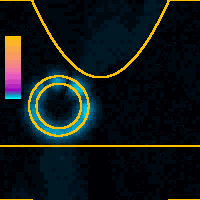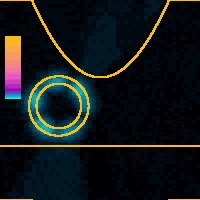
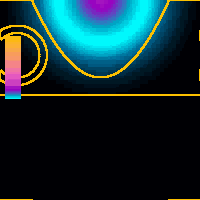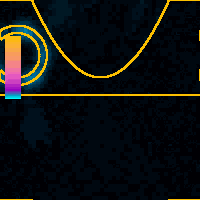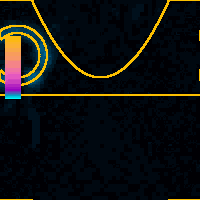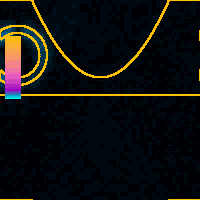
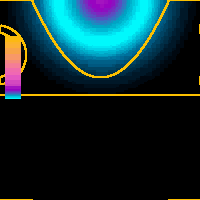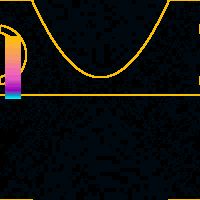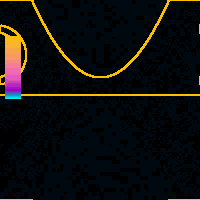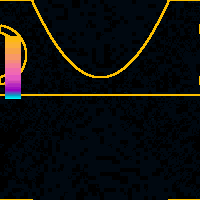
x = 0.0 nm (tip above the nanotube)The WP has to tunnel through two tunnel resistances in series, which is characteristic of resonant tunneling. The WP first flows around the NT then penetrates into the support. At later times the main mass of the probability is scattered back into the tip bulk. The probability which remained in the tube region forms standing wave patterns along the tube circumference and it is leaking into the tip and into the support in distinct impulses.The diameter of the nanotube is 1 nm which is typical of single wall nanotubes. Color scale is renormalized for each time instant only on this animation. |

|
x = 0.8 nmAs the tip moves laterally across the nanotube the simulated feedback loop regulates the height of the tip to maintain the total tunnel probability constant. Because the tunneling probability is the highest around the shortest path connecting the tip and the nanotube the majority of the probability flows out of the tip at its side. The standing wave patterns along the tube rotate because of the nonzero initial angular momentum.Color scale is global for the whole animation. |

|
x = 1.6 nmAt 1.6 nm tip displacement we can observe the switching of the tunneling point from the side to the apex of the tip. At this tip displacement the tip is already so close to the support surface that some of the WP is tunneling out from the tip apex into the support. Later another part of the WP tunnels out from the tip side into the NT.Color scale is global for the whole animation. |

|
x = 2.0 nmAt this tip displacement the tip is relatively far from the NT. The WP quickly tunnels from the tip apex into the support surface. Because this is not a resonant tunneling situation the process is very quick; we see nothing at later times.Color scale is global for the whole animation. |